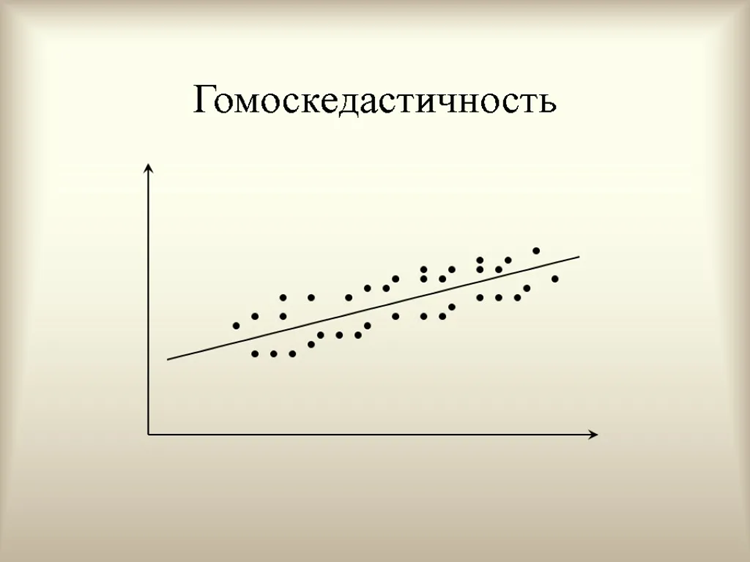
Гомоскедастичность — это фундаментальное понятие в анализе временных рядов и регрессионном моделировании, означающее равномерное распределение дисперсии случайных ошибок во времени.
Проще говоря, в условиях гомоскедастичности статистические колебания сохраняют одинаковую величину независимо от временного отрезка или значения предиктора. Это свойство имеет важное значение для корректной оценки параметров модели и построения достоверных прогнозов.
Что это такое?
С математической точки зрения гомоскедастичность означает, что дисперсия случайной ошибки εt постоянна для всех наблюдений: Var(εt) = σ² = const. Такое условие лежит в основе многих классических методов оценки, включая метод наименьших квадратов. Предположение о гомоскедастичности позволяет считать, что каждое наблюдение в выборке вносит одинаковую информацию и не искажает результат модели.
Тем не менее, в реальных данных, особенно в финансовых временных рядах, гомоскедастичность встречается редко. Как правило, дисперсия флуктуирует во времени, что приводит к гетероскедастичности — противоположному явлению, при котором ошибки модели изменчивы и зависят от факторов времени или условий. Это может быть следствием рыночных шоков, новостного фона, сезонных эффектов или других внешних воздействий. Несмотря на это, анализ на предмет гомоскедастичности остается важным этапом предварительной диагностики модели.
Игнорирование проблемы гетероскедастичности может привести к занижению ошибок прогноза, переоценке значимости коэффициентов и в целом к искаженным выводам. Поэтому при выявлении отклонений от гомоскедастичности аналитики прибегают к коррекции модели — применяя взвешенные методы оценки или строя более устойчивые к изменчивости алгоритмы.
В целом, понимание сути гомоскедастичности помогает не только лучше интерпретировать результаты анализа, но и выбрать подходящие инструменты моделирования. В современной квант-аналитике и эконометрике этот термин остается актуальным и необходимым для оценки качества модели, управления рисками и повышения точности прогнозов.
Гомоскедастичность упрощает статистический анализ, поскольку позволяет использовать стандартные оценки дисперсии и доверительных интервалов без необходимости дополнительных корректировок. В учебных и исследовательских целях модели с гомоскедастичной ошибкой часто служат отправной точкой для понимания более сложных стохастических процессов. Однако в прикладных задачах аналитики обязаны проверять это предположение с помощью специальных тестов, таких как тест Бреуша-Пагана или Уайта, чтобы убедиться в надежности полученных результатов.